union-find 算法
问题的输入是一列整数对,其中每个整数都表示一个某种类型的对象,一对整数 p q 可以被理解为「p 和 q 是相连的」 。
假设「相连」是 一种等价关系,这也就意味着它具有:
- 自反性:p 和 p 是相连的。
- 对称性:如果 p 和 q 是相连的,那么 q 和 p 也是相连的。
- 传递性:如果 p 和 q 是相连的且 q 和 r 是相连的, 那么 p 和 r 也是相连的。
目标是编写一个程序来过滤掉序列中所有无意义的整数对。
换句话说,当程序从输入中读取了整数对 p q 时,如果已知的所有整数对都不能说明 p 和 q 是相连的,那么则将这一对整数写入到输出中。如果已知的数据可以说明 p 和 q 是相连的,那么程序应该忽略 p q 这对整数并继续处理输入中的下一对整数。
动态连通性问题的应用:
网络
输入中的整数表示的可能是一个大型计算机网络中的计算机,而整数对则表示网络中的连接。 这个程序能够判定我们是否需要在 p 和 q 之间架设一条新的连接才能进行通信,或是我们可以通过已有的连接在两者之间建立通信线路;或者这些整数表示的可能是社交网络中的人,而整数对表示的是朋友关系。
变量名等价性
某些编程环境允许声明两个等价的变量名(指向同一个对象的多个引用)。在一系列这样的声明之后,系统需要能够判别两个给定的变量名是否等价。
数学集合
在更高的抽象层次上,可以将输入的所有整数看做属于不同的数学集合。在处理一个整数对 p q 时,我们是在判断它们是否属于相同的集合。如果不是,我们会将 p 所属的集合和 q 所属的集合归并到同一个集合。
API
现在使用网络方面的术语,将对象称为触点,将整数对称为连接,将等价类称为连通分量或是简称分量。
public class UF {
// 构造方法,以整数标识 [0, N - 1] 初始化 N 个触点
UF(int N);
// 在 p 和 q 之间添加一条连接
void union(int p, int q);
// p 所在的分量的标识符
int find(int p);
// 如果 p 和 q 存在于同一个分量中则返回 true
boolean connected(int p, int q);
// 连通分量的数量
int count();
}
如果两个触点在不同的分量中,union() 操作会将两个分量归并。
find() 操作会返回给定触点所在的连通分量的标识符。
connected() 操作能够判断两个触点是否存在于同一个分量之中。
count() 方法会返回所有连通分量的数量。一开始我们有 N 个分量,将两个分量归并的每次 union() 操作都会使分量总数减一。
为解决动态连通性问题设计算法的任务转化为了实现这份 API。所有的实现都应该:
- 定义一种数据结构表示已知的连接。
- 基于此数据结构实现高效的
union()、find()、connected()和count()方法。
触点和分量都会用 int 值表示,所以可以用一个以触点为索引的数组 id[] 作为基本数据结构来表示所有分量。即 i 代表触点( 0 <= i < N),id[i] 代表分量。
除了数组以外,再维护一个实例变量 count,count() 方法直接返回 count 即可。
connected() 方法的实现只需返回 find(p) == find(q) 即可,不用关心 find() 的具体实现。
所以具体的实现逻辑就在于 find() 和 union() 方法。
quick-find
保证当且仅当 id[p] 等于 id[q] 时 p 和 q 是连通的。
即在同一个连通分量中的所有触点在 id[] 中的值必须全部相同。
public class QuickFindUF {
private final int[] id;
private int count;
public QuickFindUF(int N) {
this.count = N;
this.id = new int[N];
for (int i = 0; i < N; i++) {
this.id[i] = i;
}
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
public int count() {
return count;
}
public int find(int p) {
return id[p];
}
public void union(int p, int q) {
int pID = find(p);
int qID = find(q);
if (pID == qID) {
return;
}
for (int i = 0; i < id.length; i++) {
if (id[i] == pID) {
id[i] = qID;
}
}
count--;
}
}
quick-find 的轨迹:

分析
find() 操作的速度显然是很快的,因为它只需要访问 id[] 数组一次。对于每一对输入 union() 都可能需要扫描整个 id[] 数组。union() 操作访问数组的次数在 N+3 到 2N+1 之间。
如果最后只得到了一个连通分量,那么至少需要调用 N-1 次 union(),即至少 (N+3)(N-1) ~ N^2 次数组访问。
可见算法时间效率是平方级别的。
quick-union
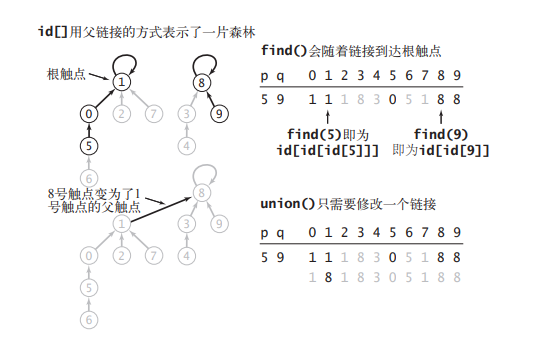
改变 id[i] 的含义,每个触点所对应的 id[] 元素都是同一个分量中的另一个触点的名称,也可能就是自身。如果 i == id[i],即为根触点。
在实现 find() 方法时,从给定的触点开始,由它的链接得到另一个触点,再由这个触点的链接到达第三个触点,如此继续跟随着链接直到到达一个根触点。
union() 中只需要修改一次「链接」即可。
public class QuickUnionUF {
private final int[] id;
private int count;
public QuickUnionUF(int N) {
this.count = N;
this.id = new int[N];
for (int i = 0; i < N; i++) {
this.id[i] = i;
}
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
public int count() {
return count;
}
public int find(int p) {
while (p != id[p]) {
p = id[p];
}
return p;
}
public void union(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
return;
}
id[pRoot] = qRoot;
count--;
}
}
quick-union 的轨迹:

分析
id[] 数组用父链接的形式表示了一片森林,一个森林就代表一个连通分量。
find() 方法访问数组的次数为 1 加上给定触点所对应的节点的深度的两倍。union() 和 connected() 访问数组的次数为两次 find() 操作(union()可能为三次)。
同样如果最后只得到一个连通分量,算法的运行时间在最坏情况下仍是平方级别的。
对于整数对 0 - i,union() 操作访问数组的次数为 2i+1 (触点 0 的深度为 i-1,触点 i 的深度为 0)。
因此,处理 N 对整数所需的所有 find() 操作访问数组的总次数为 3+5+7+…+(2N-1) ~ N^2。
加权 quick-union
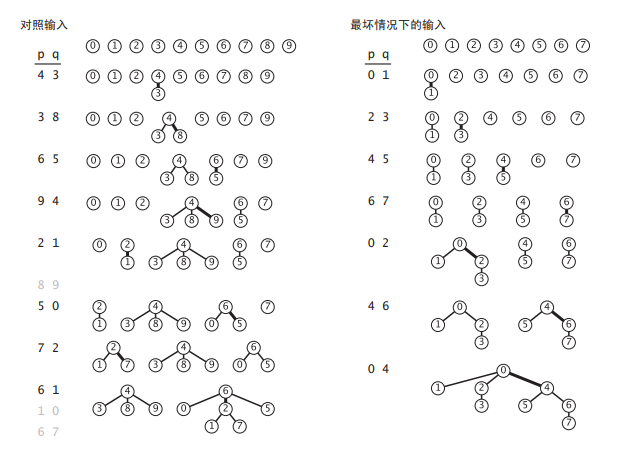
与其在 union() 中随意将一棵树连接到另一棵树,现在记录每一棵树的大小并总是选择将较小的树连接到较大的树上。
public class WeightedQuickUnionUF {
private final int[] id;
private final int[] sz; // 由触点索引的各个根节点所对应的分量的大小
private int count;
public WeightedQuickUnionUF(int N) {
this.count = N;
this.id = new int[N];
this.sz = new int[N];
for (int i = 0; i < N; i++) {
this.id[i] = i;
this.sz[i] = 1;
}
}
public int count() {
return count;
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
public int find(int p) {
while (p != id[p]) {
p = id[p];
}
return p;
}
public void union(int p, int q) {
int i = find(p);
int j = find(q);
if (i == j) {
return;
}
// 将小树的根节点连接到大树的根节点
if (sz[i] < sz[j]) {
id[i] = j;
sz[j] += sz[i];
} else {
id[j] = i;
sz[i] += sz[j];
}
count--;
}
}
加权 quick-union 的轨迹:
分析
最坏情况下,将要被归并的树的大小总是相等的(且总是 2 的幂)。这些树均含有 2n 个节点,因此高度都正好是 n。当归并两个含有 2n 个节点的树时,得到的树含有 2n+1 个节点,由此将树的高度增加到了 n+1。可见能保证对数级别的效率。
对于 N 个触点,加权 quick-union 算法构造的森林中的任意节点的深度最多为 lgN。
使用路径压缩的加权 quick-union
理想情况下,肯定希望每个节点都直接链接到它的根节点上,但又不想像 quick-find 算法那样通过修改大量链接做到这一点,可以在检查节点的同时将它们直接链接到根节点。
要实现路径压缩,只需要为 find() 添加一个循环,将在路径上遇到的所有节点都直接链接到根节点。
public class WeightedQuickUnionPathCompressionUF {
private final int[] id;
private final int[] size;
private int count;
public WeightedQuickUnionPathCompressionUF(int N) {
this.count = N;
this.id = new int[N];
this.size = new int[N];
for (int i = 0; i < N; i++) {
this.id[i] = i;
this.size[i] = 1;
}
}
public int count() {
return count;
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
public int find(int p) {
int root = p;
// 找到跟节点
while (root != id[root]) {
root = id[root];
}
while (p != id[p]) {
int temp = p;
p = id[p];
id[temp] = root;
}
return p;
}
public void union(int p, int q) {
int i = find(p);
int j = find(q);
if (i == j) {
return;
}
if (size[i] < size[j]) {
id[i] = j;
size[j] += size[i];
} else {
id[j] = i;
size[i] += size[j];
}
count--;
}
}
分析
路径压缩的加权 quick-union 算法是最优的算法,但并非所有操作都能在常数时间内完成。
| 算法 | 存在 N 个触点时成本的增长数量级(最坏情况下) | |
|---|---|---|
| union() | find() | |
| quick-find | N | 1 |
| quick-union | 树的高度 | 树的高度 |
| 加权 quick-union | lgN | lgN |
| 使用路径压缩的加权 quick-union | 非常非常地接近但仍没有达到 1 (均摊成本) | |