树状数组也叫做二元索引树(Binary Indexed Tree),或者以其发明者命名为 Fenwick 树。
正如所有的整数都可以表示成 2 的幂和,同样可以把一串序列表示成一系列子序列的和。采用这个想法,可将一个前缀和划分成多个子序列的和,而划分的方法与数的 2 的幂和具有极其相似的方式。
通过使用大节点去表示、管理一些小节点,进行查询的时候只需要查询一些大节点而不是更多的小节点。
这样可用于高效计算数列的前缀和, 区间和以及单点修改。
结构
既然叫做树状数组了,数据结构上自然还是数组,在物理空间上是连续的,即下标连续。对于两个下标通过一定关系构建关联后,就为一组父子关系,从而用「数组的形式」来表示「树的结构」。
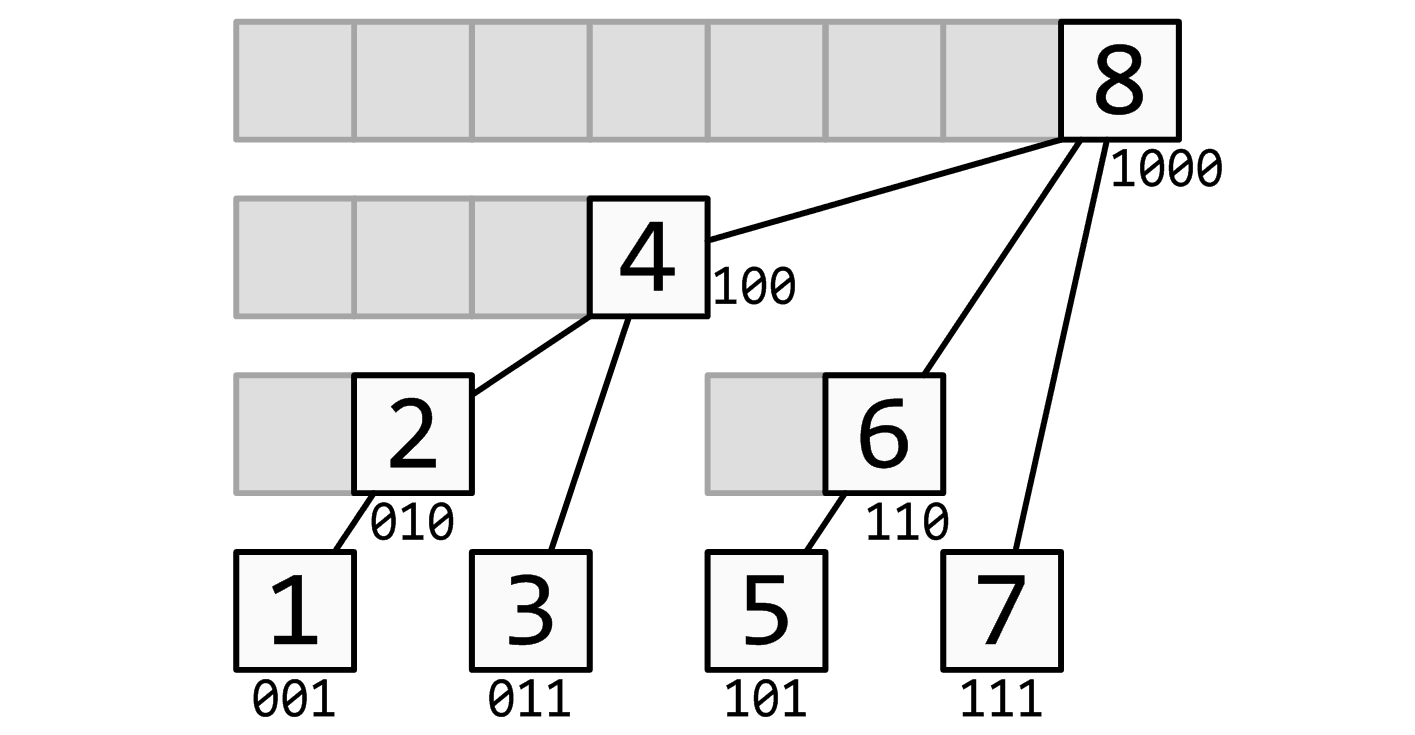
A 为普通的数组,C 代表管理 A 的数组,以维护前缀和为例子。
ai 为 A 数组中第 i 个元素,即 A[i-1]。
ci 为 C 数组中有意义的第 i 个元素,为 C[i] ,C 数组中的 index 比原数组中大 1。
c1 = a1
c2 = c1 + a2 = a1 + a2
c3 = a3
c4 = c2 + c3 + a4 = a1 + a2 + a3 + a4
c5 = a5
c6 = c5 + a6 = a5 + a6
c7 = a7
c8 = c4 + c6 + c7 + a8 = a1 + a2 + a3 + a4 + a5 + a6 + a7 + a8
ci 表示的就是数组 A 中的连续区间和:ci = sum{ aj | i - 2^k + 1 <= j <= i }
区间长度:i - (i - 2^k + 1) + 1 => 2^k
k 为 i 二进制末尾 0 的个数。用 lowbit(i) 表示 i 转为二进制后,最后一个1的位置所代表的数值。
例如 8(10) = 1000(2),lowbit(8) 返回的就是 8。从 2^0 位往前数,见到的第一个 1,也就是最后一个 1 的位置所代表的十进制数值。
可以通过 (~i + 1) & i 来计算最后一位 1 的值,对于正整数 i,其最高位为 0,-i 就是 i 按位取反后再加 1,从而简化为 i & -i。
int lowbit(int i) {
return i & -i;
}
lowbit(i) 代表节点 ci,管理的 a 节点数量。
单点修改,就是修改本节点以及逐级修改父级节点:
void update(int index, int value) {
while (index < C.length) {
C[index] += value;
index += lowbit(index);
}
}
用 A 初始化 C 可以逐级更新:
for (int i = 0; i < A.length; i++) {
update(i + 1, A[i]);
}
或者以 O(n) 建树 的方式:
for (int i = 1; i < C.length; i++) {
C[i] += A[i - 1];
int j = i + lowbit(i);
if (j < C.length) {
C[j] += C[i];
}
}
前缀和:
sum(i) = sum{ aj | 1 <= j <= i}
= a1 + a2 + a3 + ... + ai
= a1 + a2 + a(i - 2^k) + a(i - 2^k + 1) + ... + ai
= a1 + a2 + a(i - 2^k) + ci
= sum(i - 2^k) + ci
= sum(i - lowbit(i)) + ci
int sum(int index) {
int sum = 0;
while (index > 0) {
sum += C[index];
index -= lowbit(index);
}
return sum;
}